KMP算法详解+图示（附优化版）

一、KMP算法的意义

​ 在求解这样的算法问题时：已知两个字符串s1和s2，其中s2是s1的字串，请找到s2在s1中的位置。传统的寻找方法即暴力解法：分别从两个字串的第一个字符开始找起，若可以匹配就继续下一个字符；若匹配失败，s1回溯到第二个字符，s2回溯到第一个字符，依此类推……

​ 暴力解法在字串长度过大时往往时间复杂度很高，而其主要原因是因为回溯的次数太多，而KMP算法的作用就是用已知的信息量去尽可能减少回溯次数，达到简洁且迅速的效果。

二、KMP算法的步骤

1.计算字符串中每个位置之前字串的最长相等前后缀长度

（1）最长相等前后缀的概念

​ 已知一个字符串abaaba,它的前缀字串和后缀字串分别为：

前缀：a,ab,aba,abaa,abaab;

后缀：a,ba,aba,aaba,baaba;

​ 那么很明显，aba是它的最长相等前后缀，即这个字符串的最长相等前后缀长度为3。

（2）next[n]数组

​ 对于字符串abaabac，我们想要用数组next[n]中的元素next[i]来保存字符串第i个字符前的字串的最长相等前后缀的长度。

​ 首先，我们规定next[0]=-1（前面没有字串），next[1]=0(字串没有前后缀)。那么就可以得到next[n]的值：

​ a b a a b a c

next[0] [1] [2] [3] [4] [5] [6]

​ -1 0 0 1 1 2 3

2.根据next数组，对字串进行匹配

​ 创建如下图所示的两个字符串。

​ 已知在进行前六个字符的匹配时，由于都能够匹配成功，因此箭头同步向右移动。当匹配到如图所示的位置时，匹配失败了。如果按照暴力解法，那么上面的字符串应该从第一个b开始匹配，而子串需要从头匹配。

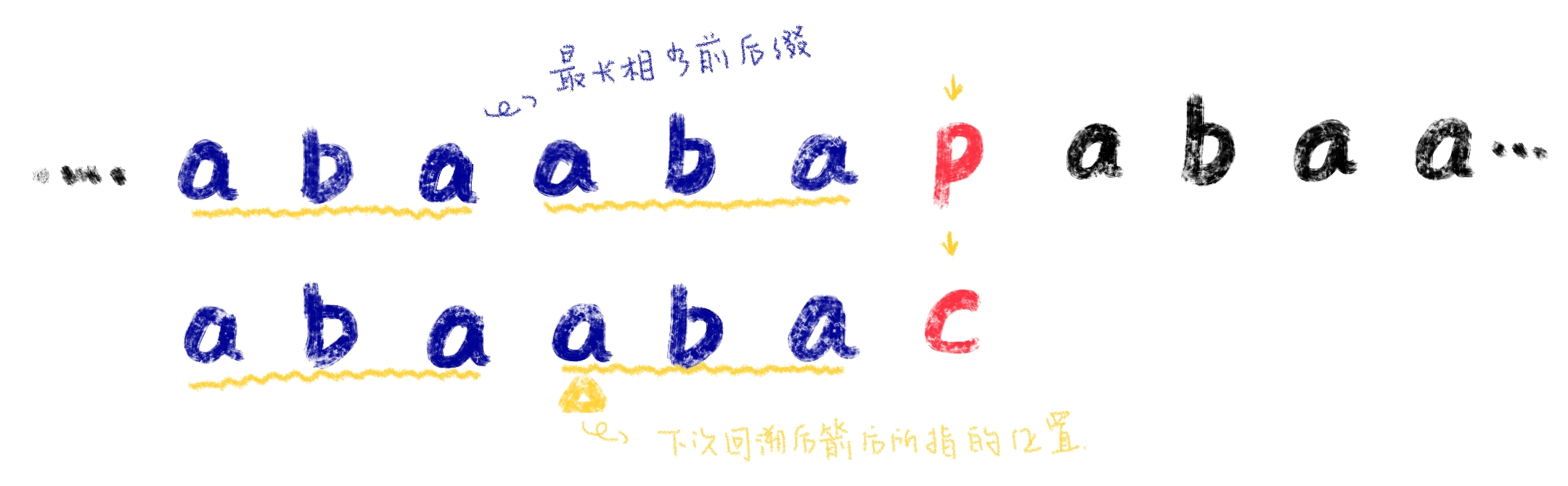
​ 而KMP算法则利用上一步我们求解的next数组，已知子串中字符c的位置是6，而next[6]=3。因此下一次匹配时，我们直接移动子串，使得子串位置为3的字符a对准箭头所在的地方，如图。

​ 接下来让我们理解一下这一步的原理是什么。我会讲解地通俗一点（可能我的理解比较浅显，但是这个思路是可以弄清楚这个算法的）。

​ 我们知道KMP算法的作用是要减少回溯的次数，那么如何减少呢？当我们已经走到图一的位置时，我们很容易发现按照暴力方法很浪费时间，因为很明显直接按图二移动是最方便快捷的。由于字符串的匹配不可能每次都让我们用眼睛看到，因此我们需要将信息存储在数组里，需要的时候就可以使用。而next数组就是存储这个重要信息的数组。比如在图一的位置，next数组可以告诉程序，在已知匹配的字符串中，前三位字符和后三位字符是相等的。而此时只有最后一位是不匹配的，因此，我们只需要把前三位平移过来，那么就可以得到图二的结果：有三位字符是匹配的，然后我们继续判断下一位是否和p匹配。既然最大相等前后缀字符串的长度为3，那么对应的，箭头就应该指向子串位置为3的字符（从0计）。

​ 以此类推，由于next[3]=1,那么相应的，箭头应该指向第二个字符b。

​ 接下来，聪明的你应该知道，箭头应该指向a了。可是这时候仍然是不匹配的，而且next[0]=-1，这时候应该怎么办呢？很简单，这时候应该将字符串的箭头向右移动了，而子串的箭头位置不变，因为它已经指向字串的第0个字符了。

三、KMP算法的代码实现

1.计算next数组

void getnext(string s,int next[])
{
    next[0]=-1;
    int i=0,k=-1;
	while(i<s.size()-1){
        if(k==-1||s[i]==s[k]){
            i++,k++;
            next[i]=k;
        }
        else{
            k=next[k];
        }
    }
}

​ 这个函数真的很不好理解。如果让我直接去想这个代码我是肯定想不到的，因此只能就着代码理清思路，这样做题的时候不至于忘记。

​ 首先，由于k的初始值是-1，所以一定会进入if函数里，这样一来，next[1]就被赋为0了。

​ 当k=-1或者s[i]=s[k]的时候，会将i和k同时右移。我们先分析，什么时候k=-1呢？只有上一次循环时k=0，并且s[0]!=s[i]时，在k=next[k]这个公式里，才会将k又赋为-1。故而此时，i+1前并无相等前后缀，也就又将next[i+1]赋为0。接着，又会判断s[i+1]与s[0]是否相等，如果相等，则i+2前最大相等前后缀长度就为1了。

​ 若前面已经有相等前后缀，此时s[i]=s[k]，那么相当于相等前后缀的延长，因此s和k会同时后移观察下一位是否也相等。

​ 比较复杂的情况如下图（理解k=next[k]）

​ 如图是一串字符串，下标i和next[i]的值分别在其上下标出。在i=6，k=3之前，可以发现最大前后缀是3，而此时s[i]=s[k]不相等。而这个函数的关键之处：k=next[k]，将k的值改变成了1（next[3]=1)。我们可以发现，如果将k和i分别向前移一位，此时k=0，i=5，而s[i]的值刚好等于s[k]。这并不是巧合。因为i=6之前最大前后缀长度为3，也就是说明字符串前三位和i=6之前的三位是相等的。而下标i=3之前的最大前后缀长度为1，也就是说明i=0、i=2、i=3、i=5这几个数的值也是相等的。所以现在我们向前回溯到，与i=6不相等的那个下标（此处为3）之前的子串中的相等前后缀，它的长度对应的下标前的子串一定和i=6前的某个后缀相等。然后我们继续比较该下标的值和i=6处的值是否相等，以此类推。

​ 如果还是不太明白可以多试几个字符串多多验证几次，推导几遍，就会渐渐思路清晰。（其实我们会发现这个思想和前面讲到的KMP思想很类似）

​ ps:while函数中之所以i<s.size()-1，是因为每次都是先i++再赋值的。

2.KMP算法的代码

int KMPinit(string s,string p)
{
	int len=p.size();
    int next[len],i=0,j=0;//初始化
    getnext(p,next);//求出next数组
    while(i<s.size()&&j<len){//跳出循环要么找完s字符串都没找到，要么已经找完了
        if(j==-1||s[i]==s[j]){//根据图示理解
            i++,j++;
        }
        else{
            j=next[j];
        }
    }
    if(j>=len){//如果跳出循环是因为已经匹配完毕，那么就可以返回位置了
        int index=i-len;
        return index;
    }
    else
        return -1;//找不到匹配项
}

四、KMP代码的优化

​ 假设子串为aaaaaab，并且字符串为aaaaaacccc。我们会发现b与c不匹配，接着便是前一位的a与c进行匹配，但是依旧不匹配，而紧接着会将前面的a依次与c匹配，得到的结果仍旧是不匹配，因此当next数组指向的字符和它本身相等时，便没有必要再匹配下去。

​ 所以我们可以把next函数做以下修正(KMP函数无需改变)

void getnext(string s,int next[])
{
    next[0]=-1;
    int i=0,k=-1;
	while(i<s.size()-1){
        if(k==-1||s[i]==s[k]){
            i++,k++;
            if(s[i]!=s[k])
            	next[i]=k;
            else
                next[i]=next[k];
        }
        else{
            k=next[k];
        }
    }
}

参考博客：CSDN（哈顿之光）