c++二叉树详解（概念+例题）

Last updated on June 3, 2024 am

二叉树的学习记录

一、二叉树相关概念

（1）二叉树的结构（照搬力扣网站）

1
2
3
4
5
6
7
8
struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode() : val(0), left(nullptr), right(nullptr) {}
	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
	TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), 	right(right) {}
};

满二叉树/完全二叉树（只有最后一层缺失，且只有右边缺失）

（2）二叉搜索树

1、简单介绍

一个节点左子树上的所有节点的值全部小于该节点，右子树上所有结点的值全部大于该节点。

作用：树如其名，二叉搜索树在搜索某个节点的值时速度更快。

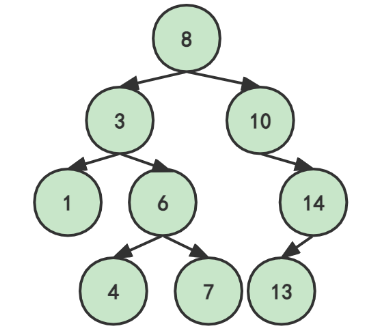
image-20240522195705342

如图，若想要找节点6，从根节点开始，小于根节点，找左子树；大于节点3，找右子树；等于节点6，找到节点。

除此之外，我们会发现这棵二叉搜索树的中序遍历：1.3.4.6.7.8.10.13.14

2、二叉搜索树的搭建

(1)笨蛋版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void insert(int k)
{
   TreeNode* temp=root;
   TreeNode* prev=nullptr;
   while(temp){
      prev=temp;
      if(k<temp->val)
         temp=temp->next;
      else
         temp=temp->right;
   }
   if(k<prev->val){
      TreeNode* curr=new TreeNode(k);
      prev->left=curr;
      curr->left=curr->right=nullptr;
   }
   if(k>prev->val){
      TreeNode* curr=new TreeNode(k);
      prev->right=curr;
      curr->left=curr->right=nullptr;
   }
}

（2）调用自身搭建

1
2
3
4
5
6
7
8
9
10
TreeNode* add(TreeNode* root,int num)
{
   if(root=nullptr)
      return new TreeNode(num);
   if(root->val>num)
      root->left=add(root->left,num);
   else
      root->right=add(root->right,num);
   return root;
}

3、二叉搜索树的例题

1>由二叉搜索树的中序遍历搭建二叉搜索树（傻眼）

方法一：总是选取中序遍历中间位置左边的数字作为根节点

1
2
3
4
5
6
7
8
9
10
11
12
TreeNode* sortedArrayToBST(vector<int>& nums) {
	return helper(nums, 0, nums.size() - 1);
}
TreeNode* helper(vector<int>& nums, int left, int right) {
   if(left>right)
      return nullptr;
   int mid=(right+left)/2;
   TreeNode* root=new TreeNode(num[mid]);
   root->left=helper(nums,left,mid-1);
   root->right=helper(nums,mid+1,right);
   return root;
}

方法二：总是选取中序遍历中间位置左边的数字作为根节点（只需mid加一）

2>找到二叉搜索树中第k大的节点值（k=cnt）

方法一：（自写）（占用额外空间）

1
2
3
4
5
6
7
8
9
10
11
12
void myinorder(TreeNode* root,vector<int>& nums){
    if(root==nullptr)
        return;
    myinorder(root->right,nums);
    nums.emplace_back(root->val);
    myinorder(root->left,nums);
}
int findTargetNode(TreeNode* root, int cnt) {
    vector<int> nums;
    myinorder(root,nums);
    return nums[cnt-1];
}

方法二：优化（空间复杂度O(1)）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int k;int res;   //必须是全局变量
void myinorder(TreeNode* root){
    if(root==nullptr)
        return;
    myinorder(root->right);
    k--;
    if(k==0){  //迭代到倒数第k节点，是第k大的节点
       res=root->val;
       return;
    }
    myinorder(root->left);
}
int findTargetNode(TreeNode* root, int cnt) {
    k=cnt;
    myinorder(root);
    return res;
}
3>前序遍历构造二叉搜索树

方法一：通过构建二叉搜索树的函数来构造

1
2
3
4
5
6
7
TreeNode* bstFromPreorder(vector<int>& preorder) {
   TreeNode* root =add(nullptr, preorder[0]);
   for (int i = 1; i < preorder.size(); i++) {
       root=add(root, preorder[i]);
   }
   return root;
}

方法二：已知二叉搜索树的中序遍历是有序的，因此我们现在知道了二叉树的前序和中序遍历（中序遍历可由前序遍历排序得出），就可以搭建了。（见下面第八道例题）

方法三：递归（分析前序遍历的特点：我们会发现，由根节点开始，第一个大于根节点的节点及其后均为右子树，中间的是左子树，依此类推）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
TreeNode* bstFromPreorder(vector<int>& preorder) {
	return mybst(preorder,0,preorder.size()-1);
}
TreeNode* mybst(vector<int>& preorder,int left,int right)
{
   if(left>right)
      return nullptr;
   int root=preorder[left];
   int mid=left;
   for(;mid<=right+1;mid++)
      if(preorder[mid]>root)
         break;
   TreeNode* node=new TreeNode(root);
   node->left=mybst(preorder,left+1,mid-1);
   node->right=mybst(preorder,mid,right);
   return node;
}
4>二叉搜索树的最近公共祖先

给定一个二叉树，找到该树中两个指定节点的最近公共祖先。（一个节点也可以是自己的祖先；最近：深度之差最小）

方法：递归（思路：找到分叉点。也就是两个节点都大于或者小于某个节点时，这个节点一定不是他们的最近公共祖先）

1
2
3
4
5
6
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { 	if(p->val<root->val&&q->val<root->val)
   	return lowestCommonAncestor(root->left,p,q);
   else
      return lowestCommonAncestor(root->right,p,q);
   return root;
}

（3）二叉树的层次遍历（自顶向下）

力扣题目链接：102. 二叉树的层序遍历 - 力扣（LeetCode）

题目描述：给你二叉树的根节点 root ，返回其节点值的层序遍历。

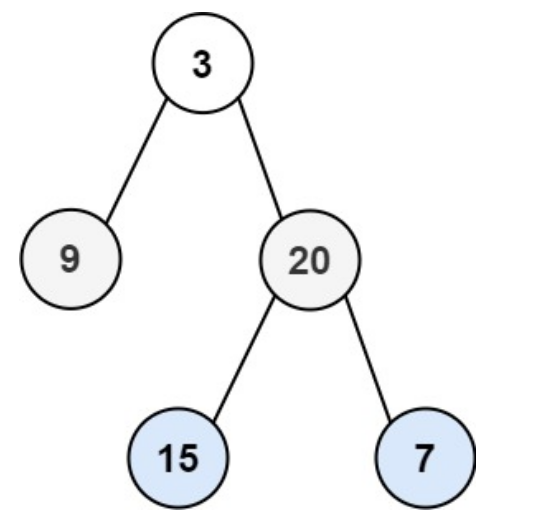
image-20240520152406792

输入：root = [ 3 , 9 , 20 , null , null , 15 , 7 ]
输出：[ [3] , [ 9 , 20 ] , [ 15 , 7 ] ]

广度优先搜索法：

（一直以为广度优先搜索都是固定的那种函数模板，函数体里总会调用自身函数，现在看来不是这样。）

（广度：一层一层全部搜索完再去下一层；深度：走到底再返回）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
vector <vector<int>> levelOrder(TreeNode* root) {
	vector<vector<int> > ret;  //存储返回值
   if(!root)
      return ret;    //空树，返回空向量
   queue <TreeNode*> q;   //存储每一层的节点
   q.push(root);    //先压入第一层（根节点）
   while(!q.empty()){   //第一层循环：表示各层的存储过程
      int curl=q.size();
      ret.push_back(vector<int>());   //每一层都要先添加一个空的向量，来存储这一层的节点值
      for(int i=1;i<=curl;++i){   //第二层循环：某一层的更新以及存储过程
         auto node=q.front();q.pop();
         ret.back().push_back(node->val);  //向最后一个向量后添加节点值
         if(node->left) q.push(node->left);  //在队列内存储下层的节点值
         if(node->right) q.push(node->right);
      }
   }
   return ret;
}

思路亦可改为每次循环新创建一个向量，然后压入每层节点值，最后再把这个向量压入二级向量中。

二级向量数组：内层是向量，向量大小不固定；外层是存储这些向量的向量。

emplace_push:据说速度要大于push_back。

二、力扣刷题记录

（1）装饰树

装饰过程：在每个父节点与其子节点之间都插入一个值为-1的节点。返回完成装饰后树的根节点。image-20240520171910175

递归法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
TreeNode* expandBinaryTree(TreeNode* root) {
   if(root!=nullptr){
      expandBinaryTree(root->left);
      if(root->left!=nullptr){
         TreeNode* T=new TreeNode(-1);
         T->left=root->left;
         root->left=T;
      }
      expandBinaryTree(root->right);
      if(root->right!=nullptr){
         TreeNode* T=new TreeNode(-1);
         T->right=root->right;
         root->right=T;
      }
   }
   return root;
}

（2）求二叉树的最小深度

力扣题目链接：111. 二叉树的最小深度 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
int minDepth(TreeNode* root) {
	if(root==nullptr)   return 0; 
   //只有左节点或右节点只能返回此节点的最小深度了（非叶子节点）
   if(root->left==nullptr)  return minDepth(root->right)+1;
   if(root->right == nullptr) return minDepth(root->left) + 1;
   return min(minDepth(root->left), minDepth(root->right)) + 1;
   //叶子节点来选择最小深度
}

（3）N叉树的前序遍历

力扣题目链接：589. N 叉树的前序遍历 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Node {
public:
	int val;
	vector<Node*> children;
};
class Solution {
public:
   vector<int> preorder(Node* root){
      vector<int> res;
      helper(root,res);
      return res;
   }
	void helper(const Node* root, vector<int> & res) {
   	if(root==nullptr)
         return;
      res.emplace_back(root->val);
      for(auto & ch:root->children)
         helper(ch,res);  //对每个子节点都进行前序遍历
   }
};

（4）克隆二叉树（递归）（无连接）

1
2
3
4
5
6
public TreeNode cloneTree(TreeNode root)
{
   if(root==null)
      return null;
   return new TreeNode{root.val,cloneTree(root.left),cloneTree(root.right)};
}

（5）翻转二叉树(递归)

226. 翻转二叉树 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
public TreeNode* invertTree(TreeNode* root)
{
   if(root==null)
      return null;
   TreeNode* left=invertTree(root->left);
   TreeNode* right=invertTree(root->right);
   root->left=right;
   root->right=left;
   return root;
}

（6）相同的树(终于自己写会的递归，只是有细节不到位)

100. 相同的树 - 力扣（LeetCode）

错误版本：

1
2
3
4
5
6
7
bool isSameTree(TreeNode* p, TreeNode* q) {
	if(p->val!=q->val)
      return 0;
   if(p==q==null)
      return 1;
   return isSameTree(p->left,q->left)+isSameTree(p->right,q->right)==2?1:0;
}

正确版本：

1
2
3
4
5
6
7
8
9
bool isSameTree(TreeNode* p, TreeNode* q) {
    if(p==nullptr&&q==nullptr)
      return true;
    else if(p==nullptr||q==nullptr)  //这个情况不要漏掉了
      return false;
    if(p->val!=q->val)   //一定要先判断是不是空再取节点值！！！！！！！
      return false;
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}

（7）对称二叉树

101. 对称二叉树 - 力扣（LeetCode）

方法一：根据前几道题解来判断（反转后如果和原树相同说明是对称的）

1
2
3
4
bool isSymmetric(TreeNode* root) {
	TreeNode root1=invertTree(root);
   return isSameTree(root1,root);
}

方法二：递归（和判断是否是相同树很像）

1
2
3
4
5
6
7
8
9
10
11
bool isSymmetric(TreeNode* root) {
	return issame(root,root);
}
bool issame(TreeNode* l,TreeNode* r)
{
   if(l==nullptr&&r==nullptr)
      return true;
   if(l==nullptr||r==nullptr)
      return false;
   return l->val==r->val&&issame(l->left,r->right)&&issame(l->right,r->left);
}

（8）由遍历构造二叉树

1>由前序遍历和中序遍历构造二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
	if(pre.empty())
      return nullptr;
   TreeNode* root=new TreeNode(pre[0]);
   //pre.erase(pre.begin());
   int size=find(in.begin(),in.end(),pre[0]);
   vector<int> prel(pre.begin()+1,pre.begin()+size+1);
   vector<int> prer(pre.begin()+size+1,pre.end());
   vector<int> inl(in.begin(),in.begin()+size);
   vector<int> inr(in.begin()+size+1,in.end());
   root->left=mybuildTree(prel,inl);
   root->right=mybuildTree(prer,inr);
   return root;
}
C++
#C++ #二叉树
c++二叉树详解（概念+例题）
http://example.com/2024/05/20/c++二叉树详解（概念+例题）/
Author
Yaodeer
Posted on
May 20, 2024
Licensed under